BruceFan's Blog

Stay hungry, stay foolish

0%

Logistic回归

发表于 Edited on

我们需要一个函数能接受所有的输入然后预测出类别，例如在两个类的情况下，这个函数输出0或1。单位阶跃函数具有这种性质，然而它的问题在于在跳跃点上从0瞬间跳跃到1，这个瞬间跳跃过程有时很难处理。幸好另一个函数也有类似性质，且数学上更易处理，这就是sigmoid函数。

sigmoid函数

sigmoid函数的具体计算公式如下：

$$
y = \frac{1}{1+e^{-z}}
$$
该函数的定义域为$(-\infty\to+\infty)$，值域为$(0, 1)$。下图是sigmoid函数的图像：

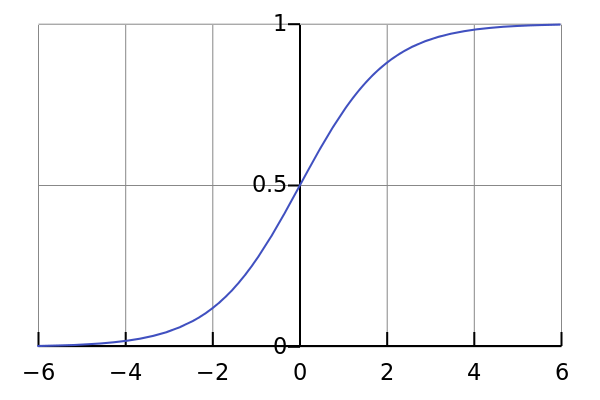
当x为0时，sigmoid函数值为0.5，随着x的增大，对应的sigmoid值将逼近于1；而随着x的减小，sigmoid值将逼近于0。

逻辑回归（logistic regression）

逻辑回归虽然名字里有回归，但实际是一种分类方法，主要用于二分类问题。生活中经常会遇到二分类问题。例如，某封电子邮件是否为垃圾邮件，某个客户是否为潜在客户，某次在线交易是否存在欺诈行为等。
为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5即被归入0类。
令$z=\boldsymbol{w^Tx}+b=w_0x_0+w_1x_1+…+w_nx_n+b$，代入sigmoid函数

$$
y=\frac{1}{1+e^{-(\boldsymbol{w^Tx}+b)}}
$$
确定了分类器的函数形式之后，接下来要做的就是求最佳回归系数了，需要用到一些最优化算法。
下面是用Python实现的逻辑回归，代码和数据 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
#coding:utf-8

import numpy as np
import os

training_sample = 'Logistic_Regression-trainingSample.txt'
testing_sample = 'Logistic_Regression-testingSample.txt'

# 从文件中读入训练样本的数据
def loadDataSet(filepath):
    dataMat = []
    labelMat = []
    f = open(filepath)
    for line in f.readlines():
        lineArr = line.strip().split()
        # 三个特征x0, x1, x2, x0=1
        dataMat.append([1.0, float(lineArr[0]), float(lineArr[1])])
        labelMat.append(int(lineArr[2]))  # 样本标签y
    return dataMat, labelMat

def sigmoid(X):
    return 1.0/(1+np.exp(-X))

# 梯度下降法求回归系数
def gradAscent(dataMatIn, classLabels):
    dataMatrix = np.mat(dataMatIn)             # 转换成numpy中的矩阵, X, 90 x 3
    labelMat = np.mat(classLabels).transpose()  # 转换成numpy中的矩阵, y, 90 x 1
    m, n = np.shape(dataMatrix)  # m=90, n=3
    lr = 0.001  # 学习率
    maxCycles = 1000
    weights = np.ones((n, 1))  # 初始参数, 3 x 1
    for k in range(maxCycles):              # heavy on matrix operations
        h = sigmoid(dataMatrix * weights)     # 模型预测值, 90 x 1
        error = h - labelMat              # 真实值与预测值之间的误差, 90 x 1
        temp = dataMatrix.transpose() * error  # 所有参数的偏导数, 3 x 1
        weights = weights - lr * temp  # 更新权重
    return weights

# 将大于0.5的归入1类，其他的为0类
def predict(y):
    preds = []
    for i in y:
        if i > 0.5:
            preds.append(1)
        else:
            preds.append(0)
    return preds
# 训练
dataArr, labelMat = loadDataSet(training_sample)  # 读入训练样本中的原始数据
A = gradAscent(dataArr, labelMat)  # 回归系数的值
# 测试
dataArr, labelMat = loadDataSet(testing_sample)
h = sigmoid(np.mat(dataArr)*A)  # 预测结果的值
print "real: "
print labelMat
print "predict: "
print predict(h)

运行结果

1
2
3
4
5
$ python logistic_regression.py
real:
[1, 0, 0, 1, 1, 1, 0, 1, 0, 0]
predict:
[1, 0, 0, 1, 1, 1, 0, 1, 0, 0]

预测结果与实际结果完全相同。
reference
《机器学习实战》