k-近邻算法

最近一直在做机器学习相关的工作，但是对机器学习的基础还没有什么太好的掌握，所以打算从头开始学习一些基本的算法，太深入的数学原理先不深究，需要用到时再补吧（说得跟真的一样）。
$k$-近邻算法，它的工作原理是：存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签，即我们知道样本集中每个数据与所属分类的对应关系。输入没有标签的新数据后，将新数据的每个特征与样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似数据的分类标签。一般来说，我们只选择样本数据集中前$k$个最相似的数据，这就是$k$-近邻算法中$k$的出处，通常$k$是不大于20的整数。最后，选择$k$个最相似数据中出现次数最多的分类，作为新数据的分类。

导入数据

创建名为kNN.py的文件：
代码清单 kNN.py

from numpy import *
import operator
# 创建数据集和标签
def createDataSet():
    group = array([[1.0, 1.1], [1.0, 1.0], [0, 0], [0, 0.1]])
    labels = ['A', 'A', 'B', 'B']
    return group, labels

这里有四组数据，每组有两个特征，labels包含了每组数据的标签，将数据点(1, 1.1)定义为类A，数据点(0, 0.1)定义为类B。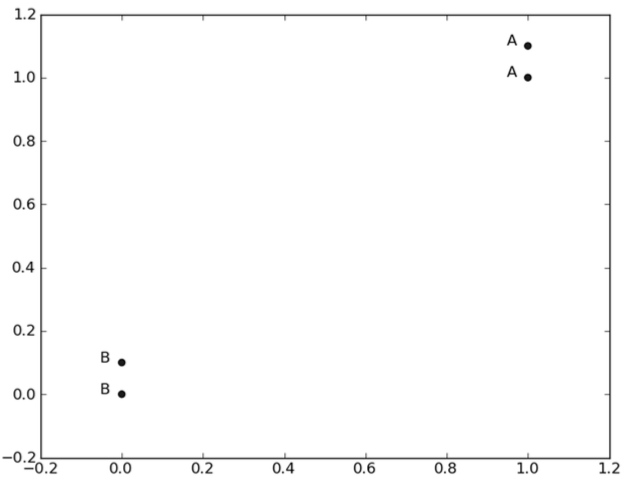

使用训练样本进行分类

添加classify0()函数：

def classify0(inX, dataSet, labels, k):
    # 计算inX这个点和样本集中点的欧式距离
    dataSetSize = dataSet.shape[0] # 数据集大小为4
    diffMat = tile(inX, (dataSetSize, 1)) - dataSet # 将输入的点复制为和数据集一样大小的4*1的矩阵
    sqDiffMat = diffMat**2 # 矩阵中的元素的平方
    sqDistances = sqDiffMat.sum(axis = 1) # 矩阵每一行求和
    distances = sqDistances**0.5
    sortedDistIndicies = distances.argsort() # 距离排序
    classCount = {}
    # 前k个距离最小的点的标签
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel, 0) + 1
    sortedClassCount = sorted(classCount.iteritems(),
            key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]
    
group, labels = createDataSet()
print classify0([0,0], group, labels, 3)

$ python kNN.py
B

对输入向量inX进行分类，训练样本集为dataSet，标签向量为labels，k表示选择最近邻居的数目。计算两点X和A的距离用欧式距离公式：
$$
d = \sqrt{(X_0-A_0)^{2}+(X_1-A_1)^{2}}
$$
例如，点(0, 0)和(1, 1)之间的距离：
$$
\sqrt{(1-0)^{2}+(1-0)^{2}}
$$
得出inX与各训练样本集中各点的距离，按距离从小到大排序，选择前k个点，这前k个点中出现最多的标签，即为inX的类。
reference
《机器学习实战》