支持向量机是一种二分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器,支持向量机还包括核技巧,这使它成为实质上的非线性分类器。支持向量机的学习策略就是间隔最大化,可形式化为一个求解凸二次规划的问题。
支持向量机学习方法包含构建由简至繁的模型:
- 当训练数据线性可分时,通过硬间隔最大化(hard margin maximization),学习一个线性的分类器,即线性可分支持向量机。
- 当训练数据近似线性可分时,通过软间隔最大化(soft margin maximization),也学习一个线性的分类器,即线性支持向量机。
- 当训练数据线性不可分时,通过使用核技巧(kernel trick)及软间隔最大化,学习非线性支持向量机。
间隔与支持向量
给定训练样本集$D={(\boldsymbol{x_1},y_1),(\boldsymbol{x_2},y_2),…,(\boldsymbol{x_m},y_m)}, y_m\in{-1,+1}$,分类学习最基本的想法就是基于训练集D在样本空间中找到一个划分超平面,将不同类别的样本分开。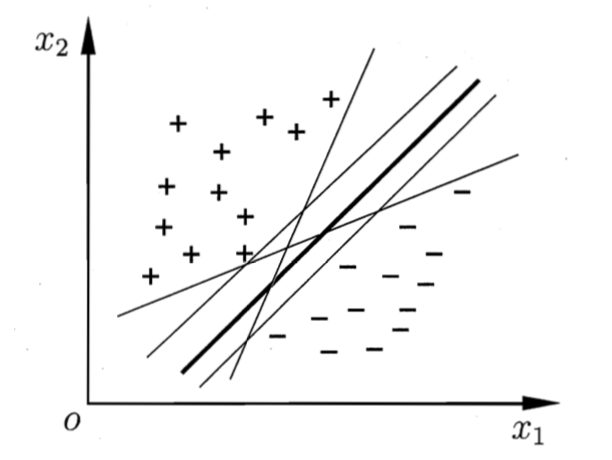
能将两类训练样本分开的超平面有很多,应该找两类训练样本正中间的划分超平面,因为该划分超平面对训练样本局部扰动的容忍性最好,产生的分类结果是最鲁棒的,对未见实例的泛化能力最强。
在样本空间中,划分超平面可通过如下线性方程来描述:
$$
\begin{aligned}
\boldsymbol{w^{T}x}+b=0
\end{aligned}\tag{1}
$$
其中$\boldsymbol{w}=(w_1;w_2;…;w_d)$为法向量,决定了超平面的方向,b为位移项,决定了超平面与原点之间的距离。划分超平面可被法向量$\boldsymbol{w}$和位移b确定,下面将其记为$(\boldsymbol{w},b)$。样本空间中任意点$\boldsymbol{x}$到超平面$(\boldsymbol{w},b)$的距离可写为
$$
\begin{aligned}
r=\frac{|\boldsymbol{w^Tx}+b|}{||\boldsymbol{w}||}
\end{aligned}\tag{2}
$$
假设超平面$(\boldsymbol{w},b)$能将训练样本正确分类,即对于$(\boldsymbol{x_i},y_i)\in D$,若$y_i=+1$,则有$\boldsymbol{w^Tx_i}+b>0$;若$y_i=-1$,则有$\boldsymbol{w^Tx_i}+b<0$。令
$$
\begin{cases}
\boldsymbol{w^Tx_i}+b \geqslant +1, & y_i=+1; \\
\boldsymbol{w^Tx_i}+b \leqslant -1, & y_i=-1.
\end{cases}\tag{3}
$$
如下图所示,距离超平面最近的这几个训练样本点使式(3)等号成立,它们被称为支持向量(support vector),这两类支持向量到超平面的距离之和为
$$
\begin{aligned}
\gamma=\frac{2}{||\boldsymbol{w}||}
\end{aligned}\tag{4}
$$
它被称为间隔(margin)。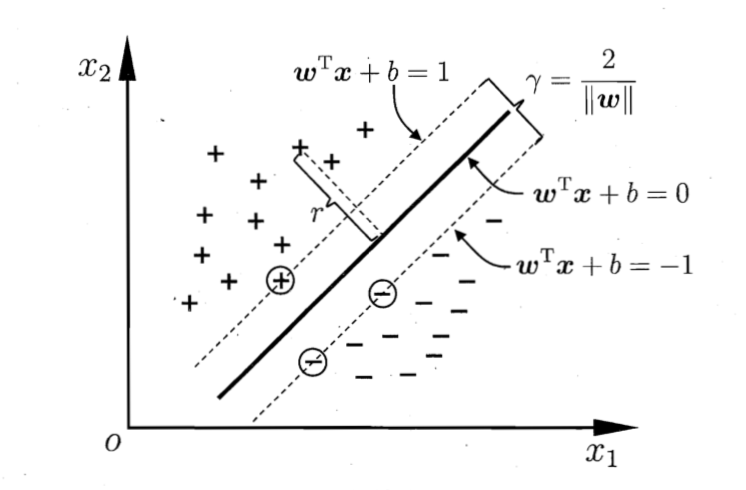
要找到具有最大间隔(maximum margin)的划分超平面,也就是要找到能满足式(3)中约束的参数$\boldsymbol{w}$和$b$,使得$\gamma$最大,即
$$
\begin{aligned}
& \max_{\boldsymbol{w},b}\frac{2}{||\boldsymbol{w}||} \\
& s.t. \ y_i(\boldsymbol{w^Tx_i}+b) \geqslant 1, \quad i=1,2,…,m.
\end{aligned}\tag{5}
$$
为了最大化间隔,需最大化$||\boldsymbol{w}||^{-1}$,等价于最小化$||\boldsymbol{w}||^2$。因此,式(5)可写为
$$
\begin{aligned}
& \min_{\boldsymbol{w},b}\frac{1}{2}||\boldsymbol{w}||^2 \\
& s.t. \ y_i(\boldsymbol{w^Tx_i}+b) \geqslant 1, \quad i=1,2,…,m.
\end{aligned}\tag{6}
$$
这就是支持向量机(Support Vector Machine)的基本型。
对偶问题
式(6)是一个凸二次规划(convex quadratic programming)问题,能直接用现成的优化计算包求解,但还有更高效的办法。对式(6)使用拉格朗日乘子法可得到其对偶问题(dual problem)。对式(6)的每条约束添加拉格朗日乘子$\alpha_i\geqslant0$,则该问题的拉格朗日函数可写为
$$
\begin{aligned}
L(\boldsymbol{w},b,\boldsymbol{\alpha})=\frac{1}{2}||\boldsymbol{w}||^2+\sum_{i=1}^m\alpha_i(1-y_i(\boldsymbol{w^Tx_i}+b)),
\end{aligned}\tag{7}
$$
其中$\boldsymbol{\alpha}=(\alpha_1;\alpha_2;…;\alpha_m)$。令$L(\boldsymbol{w},b,\boldsymbol{\alpha})$对$\boldsymbol{w}$和$b$的偏导为零可得
$$
\begin{eqnarray}
\boldsymbol{w} &=& \sum_{i=1}^m\alpha_iy_ix_i, \tag{8} \\
0 &=& \sum_{i=1}^m\alpha_iy_i. \tag{9}
\end{eqnarray}
$$
将式(8)代入(7),即可将$L(\boldsymbol{w},b,\boldsymbol{\alpha})$中的$\boldsymbol{w}$和$b$消去,再考虑式(9)的约束,就得到式(6)的对偶问题
$$
\begin{aligned}
& \max_\alpha\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\boldsymbol{x_i^Tx_j} \\
& s.t. \ \sum_{i=1}^m\alpha_iy_i=0, \\
& \alpha_i \geqslant 0, \qquad i=1,2,…,m.
\end{aligned}\tag{10}
$$
解出$\alpha$后,求出$\boldsymbol{w}$与$b$即可得到模型
$$
\begin{aligned}
f(x)&=\boldsymbol{w^Tx}+b \\
&=\sum_{i=1}^m\alpha_iy_i\boldsymbol{x_i^Tx}+b
\end{aligned}\tag{11}
$$
从对偶问题(10)解出的$\alpha_i$是式(7)中的拉格朗日乘子,它对应着训练样本$(\boldsymbol{x_i},y_i)$。注意到式(6)中有不等式约束,因此上述过程需满足KKT(Karush-Kuhn-Tucker)条件,即要求
$$
\begin{cases}
\alpha_i\geqslant 0; \\
y_if(x_i)-1\geqslant 0; \\
\alpha_i(y_if(x_i)-1)=0.
\end{cases}\tag{12}
$$
于是,对任意训练样本$(\boldsymbol{x_i},y_i)$,总有$\alpha_i=0$或$y_if(\boldsymbol{x_i})=1$。若$\alpha_i=0$,则该样本不会在式(11)的求和中出现,也就不会对$f(x)$有任何影响;若$\alpha_i>0$,则必有$y_if(\boldsymbol{x_i})=1$,所对应的样本点位于最大间隔边界上,是一个支持向量。支持向量机的一个重要性质:训练完成后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关。
式(10)是一个二次规划问题,可以用通用的二次规划算法求解,但是该问题的规模正比于训练样本数,人们通过利用问题本身的特性,提出了很多高效算法,SMO(Sequential Minimal Optimization)是最流行的一种。
SMO的思想是每次选取两个变量$\alpha_i$和$\alpha_j$,并固定其他的参数$\alpha_k$,求解式(10)获得更新后的$\alpha_i$和$\alpha_j$,不断迭代直至收敛。SMO采用了一个启发式:使选取的两变量所对应样本之间的间隔最大。仅考虑$\alpha_i$和$\alpha_j$时,式(10)中的约束可重写为:
$$
\begin{aligned}
\alpha_iy_i+\alpha_jy_j=-\sum_{k\neq i,j}\alpha_ky_k=c
\end{aligned}\tag{13}
$$
消去式(10)中的变量$\alpha_j$,则得到一个关于$\alpha_i$的单变量二次规划问题,仅有的约束是$\alpha_i\geqslant0$。这样的二次规划具有闭式解,不必调用数值优化算法即可高效地计算出更新后的$\alpha_i$和$\alpha_j$。
根据式(8)可求出$\boldsymbol{w}$,对于$b$,可以用任意一个支持向量的性质$y_s(\boldsymbol{w^Tx_s}+b)=1$来计算。当然现实任务中采用更鲁棒的做法,使用所有支持向量求解的平均值。
软间隔支持向量机
基础型的SVM的假设所有样本在样本空间是线性可分的(硬间隔),但现实中的情况通常不满足这种特性。为此,要引入软间隔(soft margin)的概念。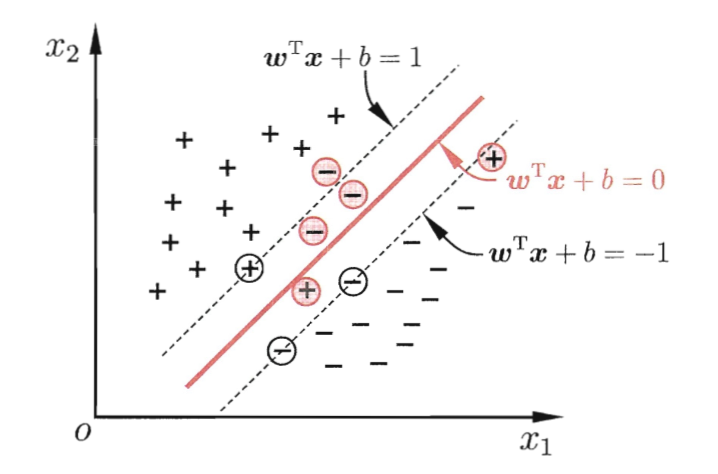
允许某些样本不满足约束 $y_i(\boldsymbol{w^Tx_i}+b)\geqslant1$,当然,在最大化间隔的同时,不满足约束的样本应尽可能少。
核函数
前面的讨论中,假设的训练样本是线性可分的,即存在一个划分超平面能将训练样本正确分类。然而现实任务中,原始样本空间内也许并不存在能正确划分两类样本的超平面。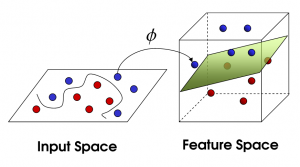
这样的问题,可将样本从原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。令$\phi(\boldsymbol{x})$表示将$\boldsymbol{x}$映射后的特征向量,在特征空间中划分超平面所对应的模型可表示为
$$
\begin{aligned}
f(\boldsymbol{x})=\boldsymbol{w^T}\phi(\boldsymbol{x})+b
\end{aligned}\tag{14}
$$
其中$\boldsymbol{w}$和$b$是模型参数,间隔最大化类似式(6)
$$
\begin{aligned}
& \min_{\boldsymbol{w},b}\frac{1}{2}||\boldsymbol{w}||^2 \\
& s.t. \ y_i(\boldsymbol{w^T}\phi(\boldsymbol{x_i})+b)\geqslant1, \quad i=1,2,…,m.
\end{aligned}\tag{15}
$$
其对偶问题是
$$
\begin{aligned}
& \max_{\alpha}\sum_{i=1}^m\alpha_i-\frac{1}{2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_j\phi(\boldsymbol{x_i})\cdot\phi(\boldsymbol{x_j}) \\
& s.t. \ \sum_{i=1}^m\alpha_iy_i=0, \\
& \alpha_i\geqslant0, \quad i=1,2,…,m.
\end{aligned}\tag{16}
$$
式中$\phi(\boldsymbol{x_i})\cdot\phi(\boldsymbol{x_j})$为$\phi(\boldsymbol{x_i})$和$\phi(\boldsymbol{x_j})$的内积。
核函数的定义: 设$\mathcal{X}$是输入空间(欧式空间$\boldsymbol{R^n}$的子集或离散集合),又设$\mathcal{H}$为特征空间,如果存在一个从$\mathcal{X}$到$\mathcal{H}$的映射
$$
\phi(\boldsymbol{x}):\mathcal{X} \to \mathcal{H}
$$
使得对所有$\boldsymbol{x_i,x_j}\in\mathcal{X}$,函数$K(\boldsymbol{x_i,x_j})$满足条件
$$
K(\boldsymbol{x_i,x_j})=\phi(\boldsymbol{x_i})\cdot\phi(\boldsymbol{x_j})
$$
则称$K(\boldsymbol{x_i,x_j})$为核函数,$\phi(\boldsymbol{x})$为映射函数。
核技巧的想法是,在学习与预测中只定义核函数$K(\boldsymbol{x_i,x_j})$,而不显式定义映射函数。通常,直接计算核函数比较容易,计算映射函数的内积很困难,因为特征空间的维数可能很高,甚至是无穷维。
reference
《机器学习》
《统计学习方法》